What Is the Difference Between Usage and Meter Read Empire District
A Gentle Introduction To Graph Theory
So many things in the earth would have never come into existence if there hadn't been a problem that needed solving. This truth applies to everything, but boy, is it obvious in the world of computer science.
Someone needed a way of keeping track of the club of things, so they played around with and created different data structures until they institute the ane that worked the all-time for the specific problem that they were trying to solve. Someone else needed a good manner of storing information, so they played around with different number systems until they plant one that worked best for the kind of information that they wanted to contain. People needed a good way of labeling and processing tasks, so they found a way to build upon the tools they had and created a way to juggle all the things that one unmarried organisation needed to practise, at any given time.
Of course, computer scientific discipline isn't the just field to innovate and build upon what came before it, but I do think that it's unique in one way: informatics's innovations rely and build upon its own abstractions.
I've talked almost abstractions a whole lot in this serial, because ultimately, that's what this series is well-nigh: finding the joy in the abstractions that lie below the things that all of united states use, every unmarried day. And, for what it'due south worth, when I say "usa", I'm only partially talking almost the states as programmers, the producers of engineering — I too mean us equally users, the consumers of engineering.
So, which astonishing abstraction shall we acquire almost adjacent? Well, now that nosotros're experts in tree data structures, it only seems correct to understand where trees came from. Trees are really a subset of something you might take already heard about: graphs. But in order to truly know why we employ graphs and what they are, we'll need to go deep down to the very roots of something that stems from discrete mathematics: graph theory.
If this is your very first foray into discrete math, fear not — it'due south mine, too! Permit's tackle it together — and try not to lose our sanity in the procedure.
Loosey–goosey graphs
When we commencement started looking at non-linear structures, we learned about their most fundamental characteristic: that their data doesn't follow an order — at least, not an obvious numerical one, similar nosotros come across in arrays or linked lists. Trees, equally we learned, offset with a root node, and might connect to other nodes, which ways that could contain subtrees within them. Trees are defined by a certain set of rules: one root node may or may non connect to others, but ultimately, it all stems from 1 specific place. Some trees have even more than specific rules, like binary search copse, which can but ever have 2 links to 2 nodes at whatever given fourth dimension.
But what if nosotros did something kind of crazy and only…threw these rules out the window? Well, equally it turns out, we totally can do that! It'south simply that nosotros wouldn't be dealing with trees anymore — we'd be dealing with something called a graph.
Trees are zip more than restricted types of graphs, just with many more than rules to follow . A tree will always be a graph, but non all graphs will be trees.
Then, what is it that makes a tree different from the big umbrella of graphs?
Well, for one matter, a tree can only flow in i direction, from the root node to either leaf nodes or child nodes. A tree can also only accept 1-manner connections — a child node can merely have one parent, and a tree can't have any loops, or cyclical links.
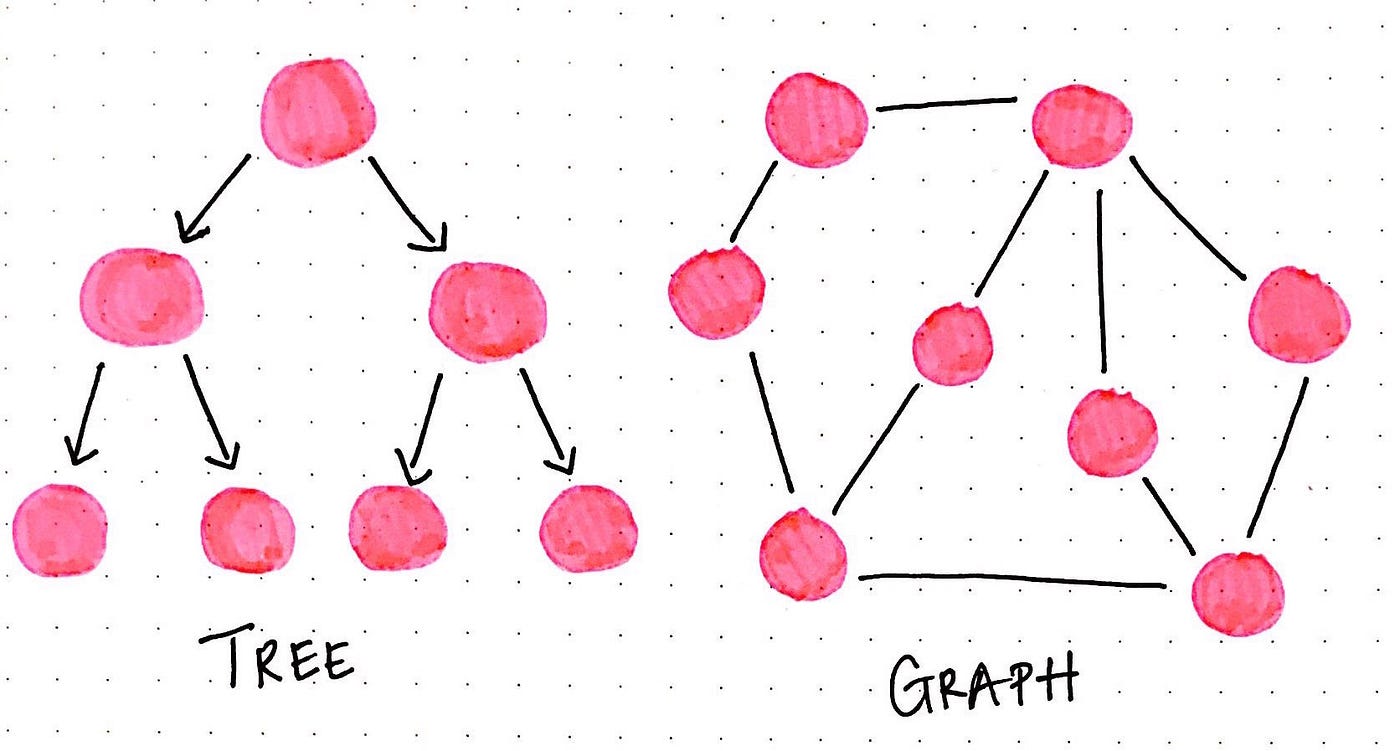
With graphs, all of these restrictions go straight out the window. Graphs don't accept any concept of a "root" node. And why would they? Nodes tin be connected in any way possible, really. Ane node might be connected to five others! Graphs also don't have any notion of "one-directional" flow — instead, they might take management, or they might take no direction whatsoever. Or, to complicate matters farther, they could take some links that take direction and others that don't! But nosotros won't get into that today.
Let's stick with the simple stuff to start.
Graphs with management, and graphs without
Okay, so we know that graphs pretty much break all the rules that we know. All the same, there is one feature that every graph must have: every graph always needs to have, at the very least, 1 single node. Just as how copse demand at least ane root node in gild to be considered a "tree", similarly, a graph needs at least a single node in society to be considered a "graph". A graph with simply i node is usually referred to as a singleton graph, although we won't actually exist dealing with those.
Nigh of the graphs nosotros'll be dealing with are a bit more complex. But, don't exist worried — we won't be diving into the super complicated graphs today. And trust me, some graphs really are complicated!
Instead, allow's wait at the 2 types of graphs that are pretty piece of cake to spot, and also pretty mutual in graph theory problems: directed graphs, and undirected graphs.
As we know, there are no real rules in the fashion that one node is connected to another node in a graph. Edges (sometimes referred to as links) tin connect nodes in whatever way possible.
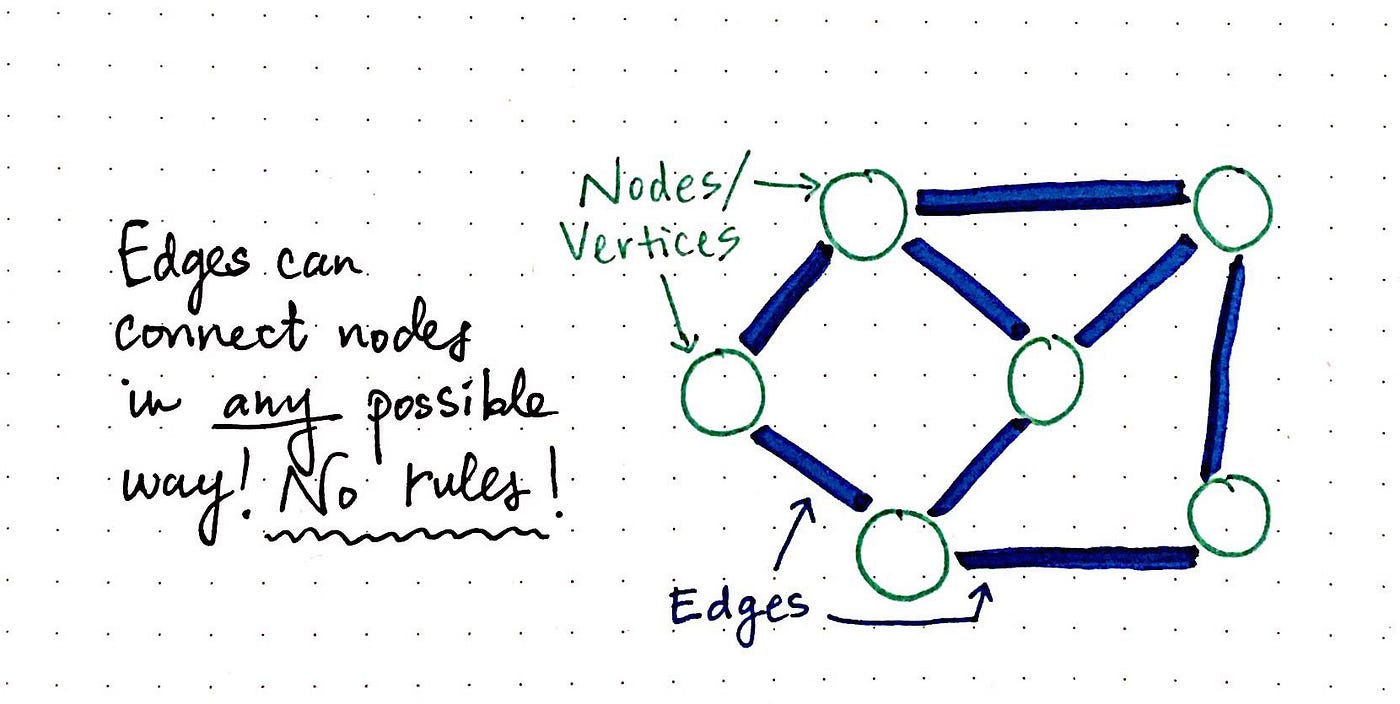
The different types of edges are pretty important when information technology comes to recognizing and defining graphs. In fact, that's one of the biggest and most obvious differentiators between i graph and another: the types of edges that it has. For the most part (aside from i exception, which nosotros won't cover today), graphs can have 2 types of edges: a edge that has a direction or period, and an border that has no management or menstruation. We refer to these every bit directed and undirected edges, respectfully.
In a directed edge, two nodes are connected in a very specific way. In the example below, node A connects to node B; there is only 1 way to travel between these 2 nodes — just ane direction that we tin can go. It's pretty mutual to refer to the node that we're starting from every bit the origin, and the node that we're traveling to as the destination. In a directed edge, we can merely travel from the origin to the destination, and never the other way around.
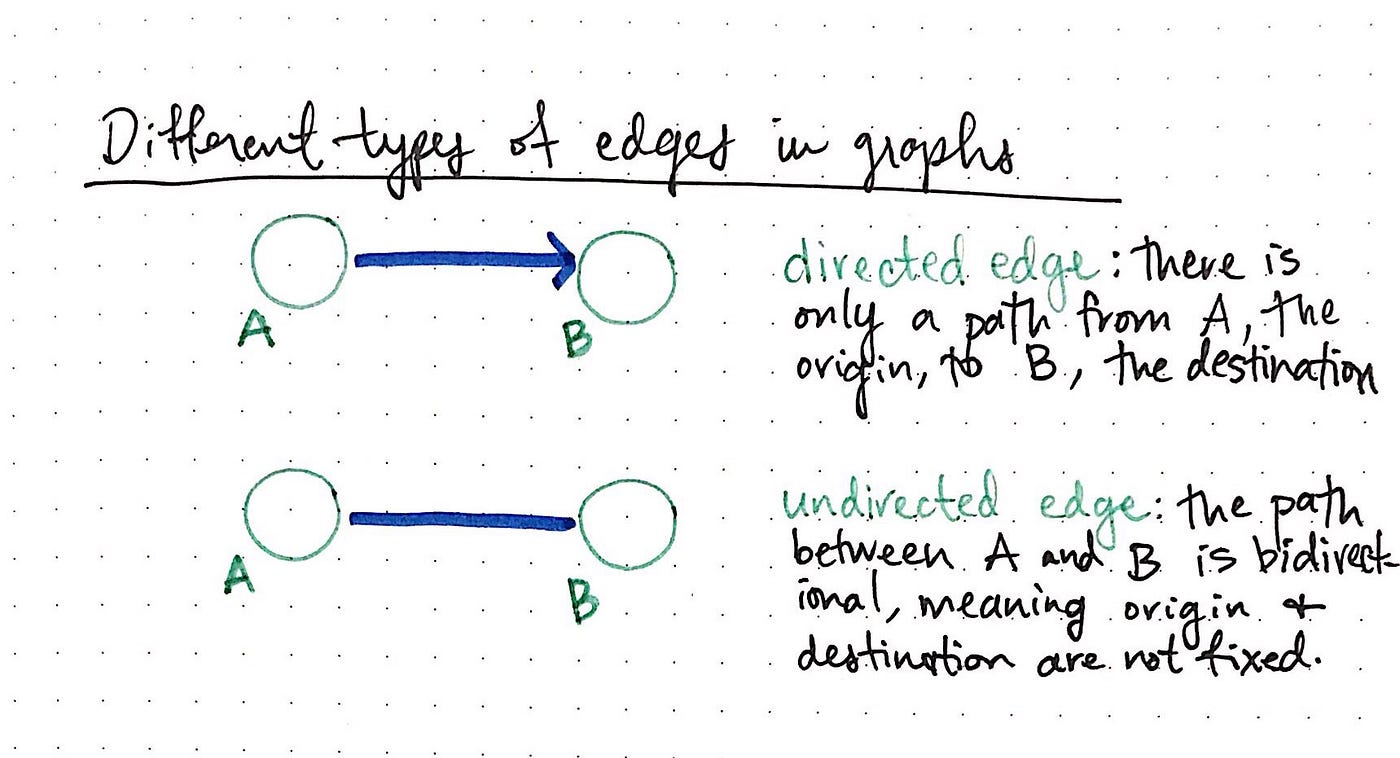
Withal, information technology's an entirely different story with undirected edges. In an undirected edge, the path that nosotros tin travel goes both means. That is to say, the path between the 2 nodes is bidirectional, meaning that the origin and destination nodes are not fixed.
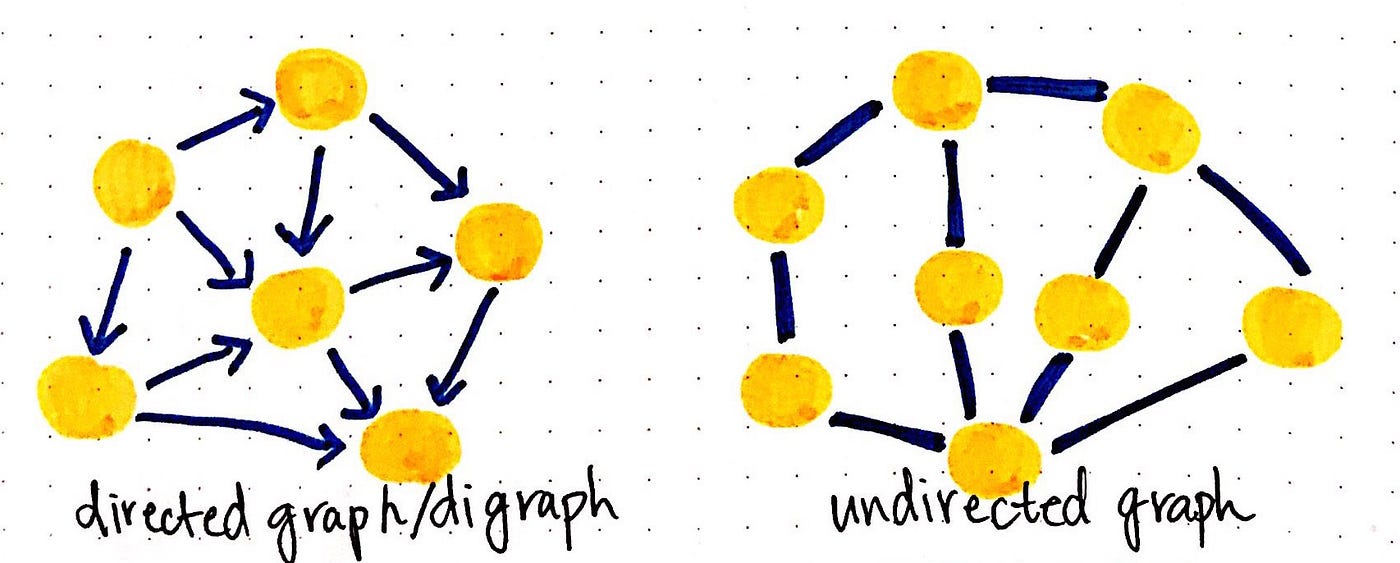
This differentiation is actually pretty important, considering the edges in a graph determine what the graph is chosen. If all of the edges in a graph are directed, the graph is said to exist a directed graph, as well called digraph . If all of the edges in a graph are undirected, the graph is said to be — y'all guessed information technology — an undirected graph! Get figure, right?
This is all very cool, only at this point, I desire to know ii things — where did all of this graph stuff come from, exactly? And…why should we intendance?
Let's investigate.
Tread lightly: we're in graph country at present
Estimator scientific discipline loves to infringe stuff. More specifically, it has borrowed a lot of concepts from logic and mathematics. As it turns out, this is the example with graphs.
Graph data structures as we know them to be reckoner scientific discipline actually come from math, and the report of graphs, which is referred to as graph theory.
In mathematics, graphs are a mode to formally stand for a network, which is basically just a drove of objects that are all interconnected.
As information technology turns out, when figurer scientists applied graph theory to lawmaking (and ultimately implemented graphs equally information structures), they didn't change a whole lot. Then, a lot of the terms that we use to draw and implement graphs are the exact terms that we'll find in mathematical references to graph theory.
For example, in mathematical terms, nosotros describe graphs as ordered pairs. Remember loftier school algebra, when nosotros learned about (10,y) ordered pair coordinates? Similar deal here, with one deviation: instead of 10 and y, the parts of a graph instead are: v , for vertices, and e , for its edges.
The formal, mathematical definition for a graph is only this: Chiliad = (V, E). That's information technology! Really. I promise.
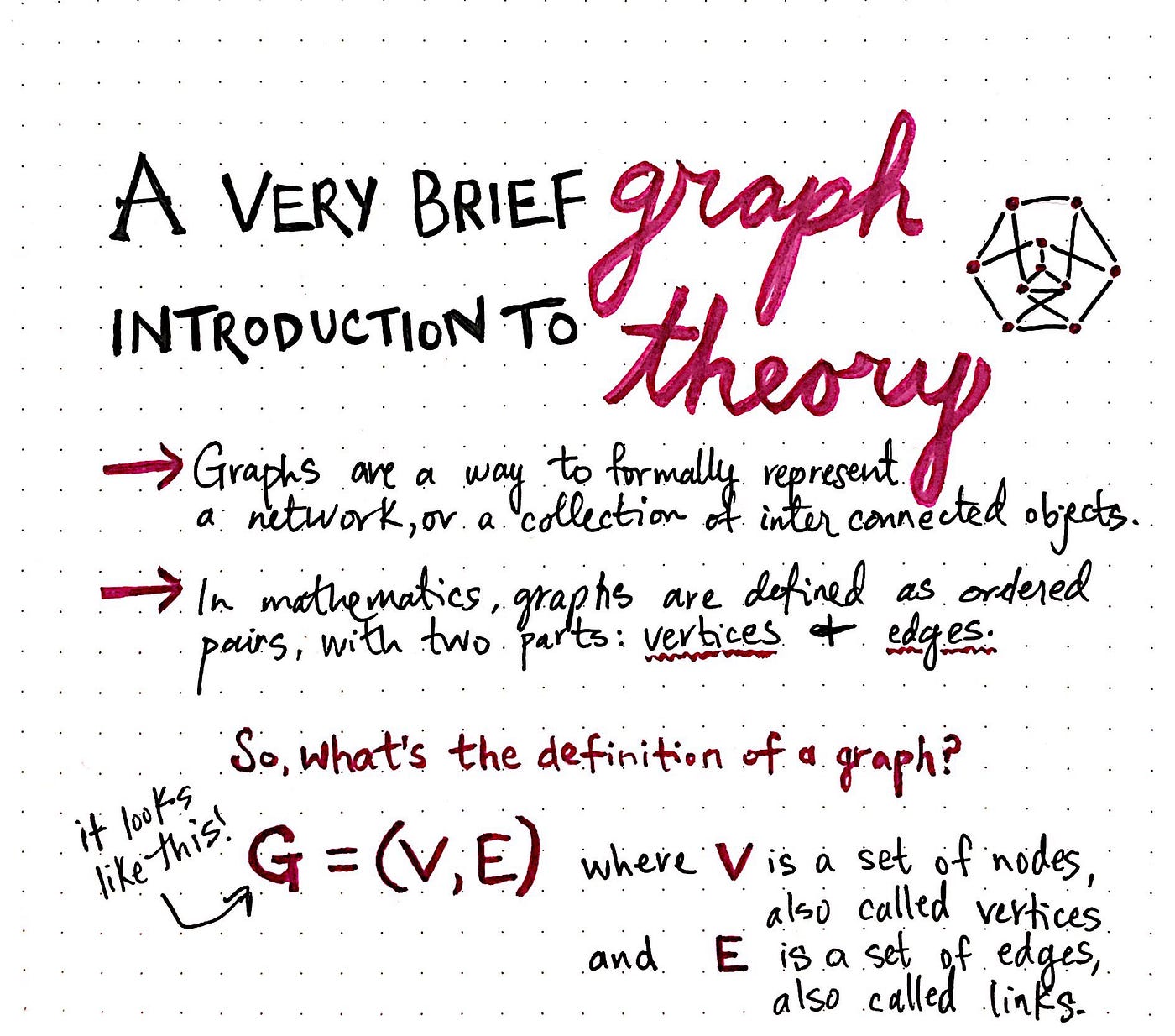
Just hang on a second — what if our graph has more one node and more than ane edge! In fact…it will pretty much ever have multiple edges if it has more than i node. How on earth does this definition piece of work?
Well, information technology works because that ordered pair — (V, Due east) — is actually made up of two objects: a prepare of vertices, and a set of edges.
Okay, that makes more sense to me now. Just it would be a whole lot clearer if I had an example and actually wrote out the definition of a graph! And so nosotros'll do just that. In the example below, we have an undirected graph, with 8 vertices, and eleven edges.

So what's going on here?
Well, we wrote out our ordered pair (Five, E), but because each of those items is an object, nosotros had to write those out too. Nosotros defined V every bit an unordered set of references to our 8 vertices. The "unordered" role is really important hither, considering remember, unlike trees, there is no hierarchy of nodes! Which means that we don't need to guild them, since order doesn't matter here.
We also had to define East every bit an object, which contains a bunch of border objects within it. Detect yet over again that our edge objects are too unordered. Why might that be? Well, what type of graph is this? Is at that place any direction or flow? Is there a fixed sense of "origin" and "destination"?
Nope, there's not! This is an undirected graph, which means that the edges are bidirectional and the origin node and destination node are not stock-still. Then, each of our edge objects are too unordered pairs.
This particularity, of course, leads united states of america to wonder: what if this were a directed graph? Time for some other example! Here's a directed graph, with iii vertices and three edges:
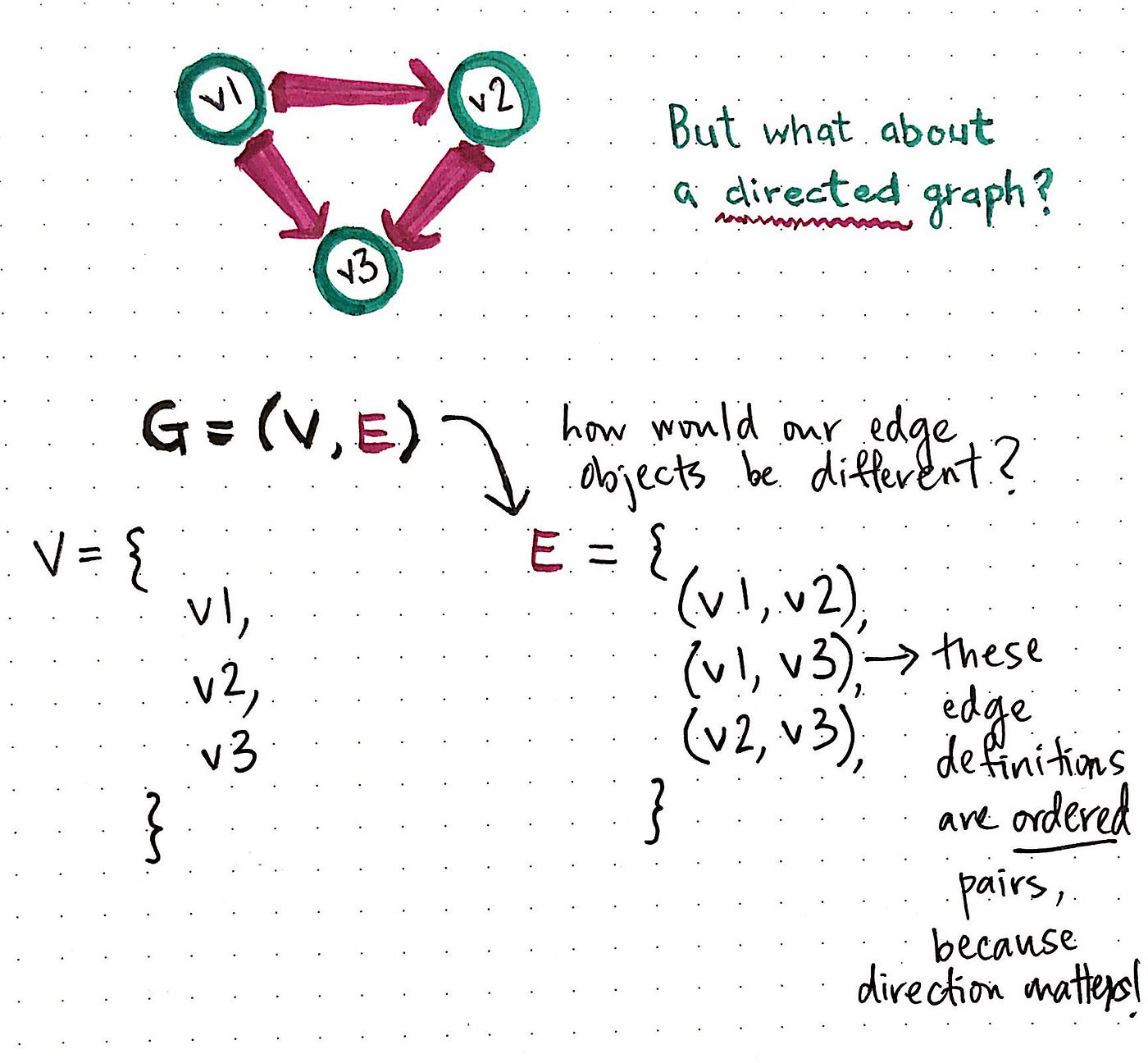
The style we define the vertices here doesn't await whatsoever different, but allow'due south look more than closely at our edge definition. Our border objects in this case are ordered pairs, because direction actually matters in this case! Since we tin can but travel from the origin node to the destination node, our edges must be ordered, such that the origin node is the first of the 2 nodes in each of our edge definitions.
Cool, and so that's how we define graphs. Only…when would we ever actually apply graphs? Well, you probably used one today. You might just not know information technology notwithstanding! Time to change that.
Super social graphs
Graphs are all effectually us, we merely don't always see them for what they are.
In fact, by the very human action of reading this post, you are literally on a graph right at present. The web is a massive graph structure! When we click between websites and navigate back and forth between URLs, we're really just navigating through a graph. Sometimes those graphs accept nodes with edges that are undirected — I can become back and along from one webpage to another — and others that are directed — I tin can only become from webpage A to webpage B, and never the other manner around.
Simply there's an even amend instance that beautifully illustrates our daily interactions with graphs: social networks.
Facebook, a massive social network, is a type of graph. And if we think more about it actually functions, we first to amend empathize how we tin define, and exactly what type of graph it is. On Facebook, if I add yous as a friend, you must accept my request. It'south not possible for me to exist your friend on the network without you too being mine. The human relationship betwixt ii users (read: nodes or vertices in graph terms!) is bidirectional. There'southward no concept of an "origin" and a "destination" node — instead, you lot're my friend and I am yours.
Can you guess what type of graph Facebook is implemented as?
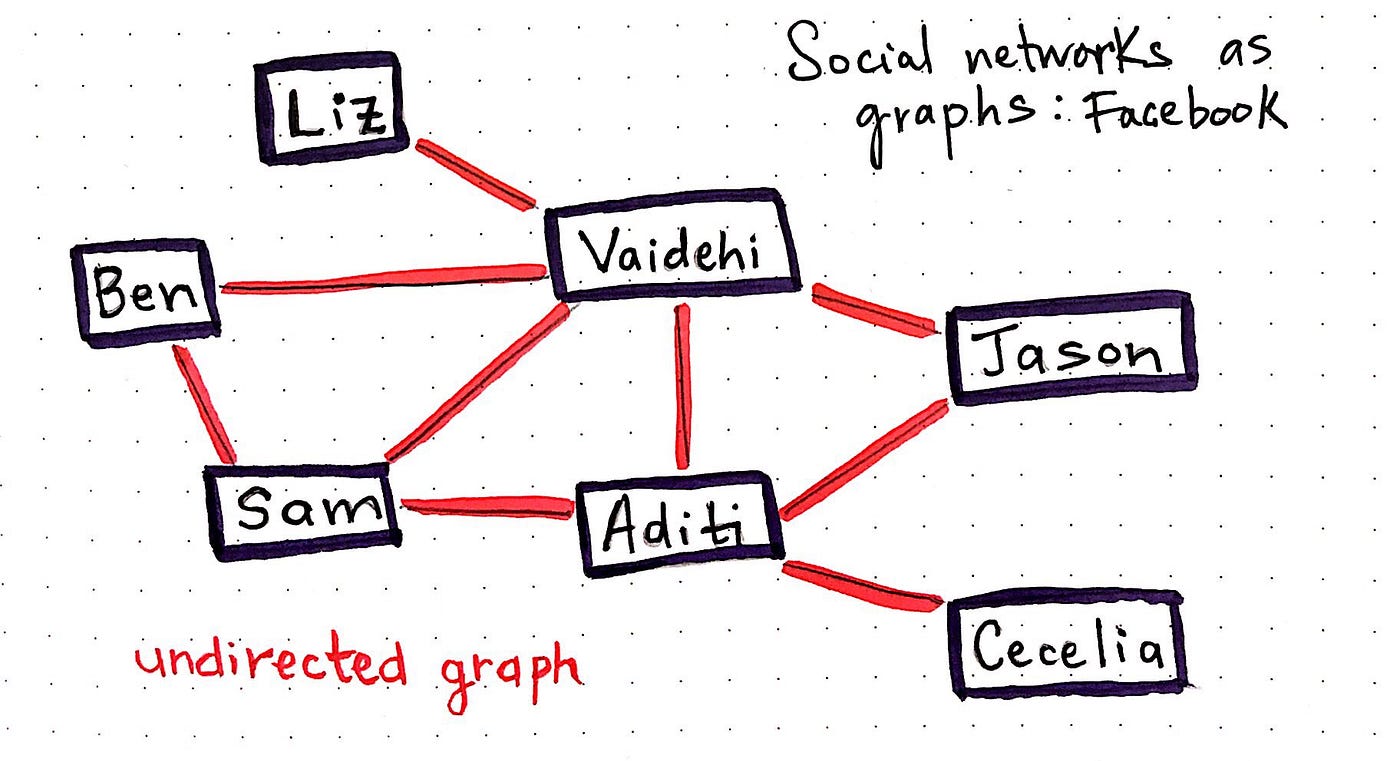
If you guessed undirected graph, so you're correct! Well done. Relationships are 2-way, and then if we were to ascertain Facebook's friend network as a graph, its edges would all end up existence unordered pairs when we wrote them out.
Twitter, on the other manus, works very differently from Facebook. I can follow yous, but you might non follow me dorsum. Case in point: I follow Beyonce, but she definitely does not follow me back (sadly).
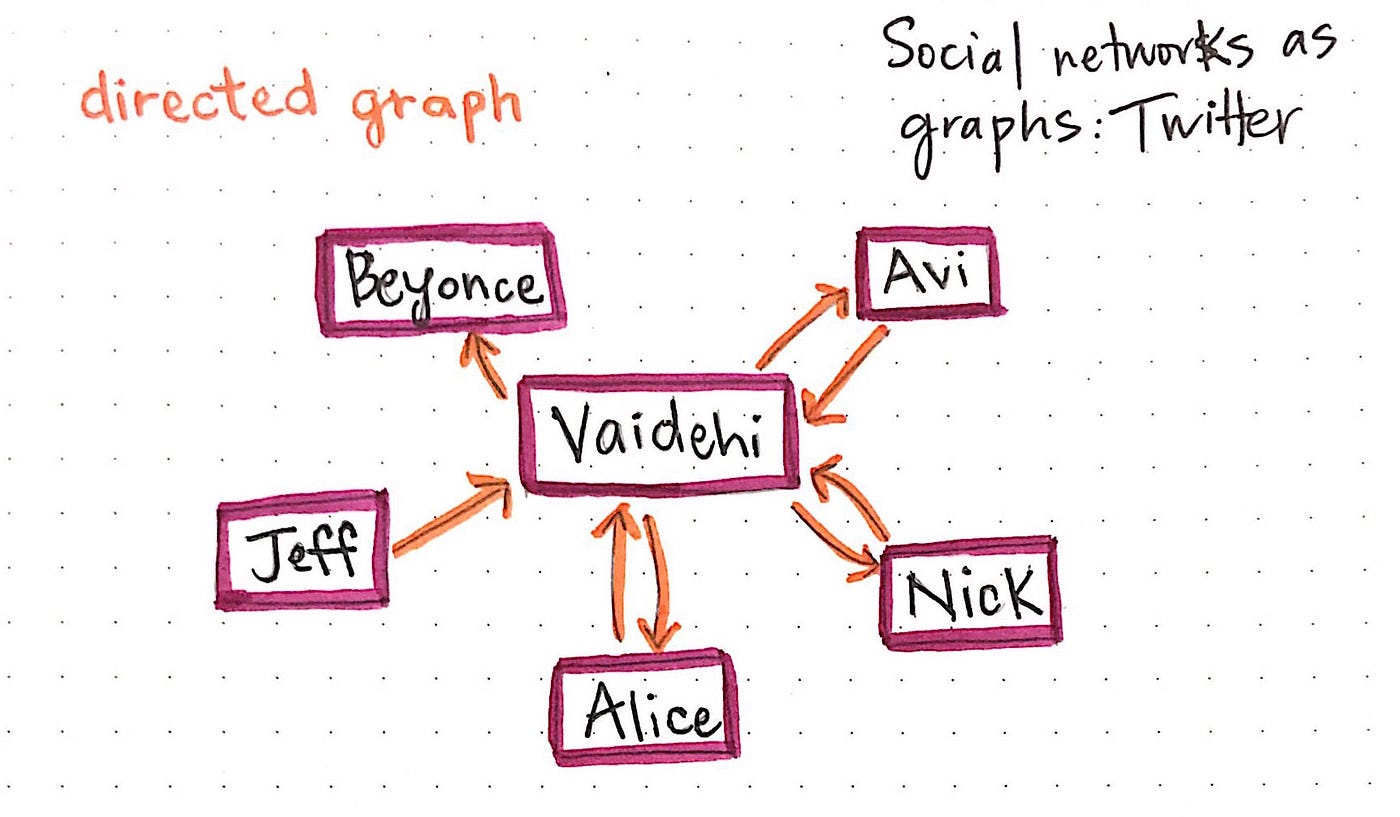
We could represent Twitter as a directed graph. Each edge nosotros create represents a one-way relationship. When you follow me on Twitter, yous create an edge in the graph with your account as the origin node, and my business relationship as the destination node.
And so what happens when I follow you back? Practice I alter the border yous created when you followed me? Does it suddenly become bidirectional? Well, no, because I could unfollow y'all at any given indicate. When I follow you back on Twitter, I create a 2d border, with my account every bit the origin node and yours as the destination.
The same model applies to Medium, as well, which lets you follow and unfollow authors! In fact, this network model is all over the identify. And all it is, once we abstract all the layers away, is a graph. And truly, what a powerful matter it is.
Resources
Lots and lots of entire books accept been written about graphs. I certainly didn't comprehend plenty information here to make full a volume, just that doesn't hateful you can't keep learning about graphs! Fill your listen with more graph theory awesomeness, starting with the great links below.
- Divergence between trees and graphs, Poonam Dhanvani
- What's the difference between the data structure tree and graph?, StackOverflow
- Applications of Graph Theory In Informatics: An Overview, Southward.M.Shirinivas et. al.
- Graph Traversal, Professor Jonathan Cohen
- Information Structures: Introduction To Graphs, mycodeschool
Source: https://medium.com/basecs/a-gentle-introduction-to-graph-theory-77969829ead8
0 Response to "What Is the Difference Between Usage and Meter Read Empire District"
Enregistrer un commentaire